はじめに
割合についての有名な話として、以下のようなものがある。
リンゴとみかんが合わせて100コある。98 %がリンゴである。リンゴの割合が99%となるようにするためには、 リンゴをいくつ足せばよいか
答えを求めるのはそうむずかしくない。みかんの数は2個でずっと変わらない。そして、最終的にリンゴはみかんの99倍 の個数あるのだから、
\[ 2\times 99=198 \]
のリンゴがあればよい。既に98コあるから、
\[ 198-98=100 \]
で、リンゴを100コ足せばよい。
この話の主題は、「全部で100コある果物のうち、リンゴの割合をたった1 %上昇させるために、 もう100コもリンゴを用意しなければならない」ことにある。割合を上昇させる手間は、感覚よりもずっと多くなることがある。 この話を数式を使って抽象化し、果物の数やリンゴの数がいくつで、割合をいくつ上昇させたいときに、 追加でどれくらいのリンゴが必要なのかを考えてみる。おそらく高校数学の範囲で済むだろう。
文字の定義
多重集合 \(U\) の元 \(N\) コのうち、割合\(r\) 、個数でいえば \(rN\) コが \(a\) という元である (言い換えれば、 \(a\) の重複度が \(rN\) である)。 このとき、元 \(a\) を \(x\) コ集合 \(U\) に追加する(i.e. \(a\) の重複度を \(x\) 増やす)と、 集合 \(U\) の元全体に占める元 \(a\) の割合が\(d\) 上昇したとする。この事象を定式化し、\(x\) を求める。
リンゴやみかんとの対応は?
人によっては、ガチガチの数学用語で書かれると意味わからんと思うかもしれない。 特に多重集合はあまり一般的ではないし、なんなら集合はあまりこういう使いかたはしない(私の観測範囲では、 集合の元を増減させることはあまりしない)。そういう人のために、もしくはこの定式化が納得がいかない人のために、 はじめに書いた果物の状況と文字を対応させておく。
多重集合 \(U\) は、用意した果物に相当し、全部で \(N\) 、つまり \(100\) コある。そのうち、割合 \(r\) 、つまり0.98 (98 %)が \(a\) 、つまりリンゴである。残りはみかんに相当する。そこで、リンゴ、つまり \(a\) の割合を98 % から99 %にしたい。 これは1 %上げたいということだから、 \(d\) は0.01となる。ここで、追加したリンゴの数が \(x\) コということだ。
前段落で現実の問題と文字と対応させたが、これだと結局数学の方を理解していないとピンとこない可能性があるので、 果物の例で完全な問題文を書いておく。
かご \(U\) には、 \(N\) コの果物が入っている。そのうち、 割合 \(r\) 、個数でいえば \(rN\) コがリンゴ(\(a\) とも呼ぶ)である。 このとき、リンゴを \(x\) コかご \(U\) に追加すると、 かご \(U\) に乗っている果物全体に占めるリンゴの割合が \(d\) 上昇した(つまり割合が \(r\) から \(r+d\) になった)。 \(x\) を求めよ。
解く
\(N\) コの果物に \(x\) コの \(a\) (リンゴ)を追加したあとの総数 \(N+x\) のうち、割合 \(r+d\) が \(a\) に相当する。 ここで、\(a\) の個数は、元あった \(rN\) コと追加した \(x\) コを合わせて \(rN+x\) である。 この二つから追加後のリンゴの数について等式を立てると、
\[ (r+d)(N+x)=rN+x \]
これを \(x\) について解く。 \(x\) について解くためには、式にある全ての \(x\) を分配則によって \(x\) との積の形の項(\(5x\) や \(bx\) のような形) にすればよいので、 \((r+d)\) を \((N+x)\) の2項に分配し
\[ (r+d)N+(r+d)x=rN+x \]
とする。 等式変形により、 \(x\) との積の形の項を左辺、それ以外を右辺にもっていけば、
\[ (r+d-1)x=rN-(r+d)N \]
右辺を整理すれば
\[ (r+d-1)x=-Nd \]
\(x\) にかけられている邪魔な \(r+d-1\) で両辺で割れば、
\[ x=N\frac{d}{1-r-d} \]
となる(分母と分子両方に \(-1\) をかけて、両方正になるようにしている)。
確かめる
さて、この式が本当に正しいか確かめたい。方法はいくつかある。まずはひたすら代入して正しい答えが出るか確認すること。 はじめに示した果物の例を使うと、
\[ x=100\times\frac{0.01}{1-0.98-0.01}=100 \]
となる。どうやら正しそうだ。
次に試すことは、極端な例を考えることだ。リンゴが極端に少ないとき、追加で必要な量も極端に少なくなりそうだ。 たとえば、1000000コの果物のうちリンゴが1コ(つまり \(r=0.000001\))のとき、リンゴを1コ追加すると、 1000001コのうちリンゴが2コになるわけだ。果物の数は1.000001倍にしかなっていないが、リンゴの個数は2倍に なっている。これはリンゴの割合がほぼ2倍になっていると考えて差し支えないだろう。 適当に代入してみよう。 \(d=0.01\) 、つまり割合を1 %上げることを考えよう。
\[ x=1000000\times\frac{0.01}{1-0.000001-0.01}\fallingdotseq 10101 \]
10101コ追加すればいいようだ。これを多いと捉える人もいるかもしれないが、1000000コのうちの10101コであるので、 元の果物の1 %ほどである。割合を1 %上げるためには、絶対に元の量の1 %は必要(なぜなら、みかんをリンゴに置き換えて いく時、ちょうど全体の果物の1 %を置き換えれば1 %上がる。今回はみかんが残っていて、リンゴの割合が増えるのを 邪魔するはずだから、それよりもリンゴはたくさん必要になるはず)なのだから、これはほぼ最低量だ。 極端に少ないことがわかった。特に矛盾はなさそうだ。
同様に、リンゴが極端に多いとき、追加で必要な量も極端に多くなりそうだ。 たとえば、果物が1000000コの果物のうちリンゴが999999コ(つまり \(r=0.999999\))のとき、リンゴを1コ追加しても、 果物の数は10000001コ(つまり1.000001倍)、リンゴの数が1000000コ(つまり1000000/999999≒1.000001000001倍)にしかならない。 リンゴは大量に必要そうだ。さっきと同様に、 \(d=0.01\) 、つまり割合を1 %上げることを考えよう。 ただし、今例に出した数字では、1 %上がったら100 %を越えてしまうので、リンゴの量を少し減らして、 989999コ(つまり \(r=0.989999\))としておこう。これなら1 %上がってもリンゴの割合は99.9999 %だ。
\[ x=1000000\times\frac{0.01}{1-0.989999-0.01}=10000000000(=10^{10}) \]
なんと、10000000000コも必要らしい。つまり、元の果物の10000倍のリンゴを用意しなければならない。 極端に多くなっていることがわかった。こちらも矛盾はなさそうだ。
どんなことがわかるか
さて、式が正しそうだとわかったところで、式がどんなことを表しているか考えよう。
まず、 \(x\) が \(N\) に比例している。これは当然で、果物が2倍あれば、足す量も2倍必要だろう。 当たり前だが、もちろんこのことも頭の片隅にあったほうがよい。割合を変化させるのは、 母数が多いとそれに比例して大変になる。
次に気になるのは \(r\) についてだろう。割合 \(r\) が大きくなるほど \(x\) が大きくなりそうだ。 双曲線を知っている人はグラフの形がすぐに浮んでくるかもしれないが、そういう人ばかりではないので、 とりあえず \(d=0.01\) として、 \(r\) - \(x\) グラフを書いてみる。 ここでめちゃめちゃ綺麗にグラフが書けるツールを紹介するのも悪くはないが、 この記事の主題はいろんな人にこういう考え方や手法を実践してもらうことであり、 これくらいのことなら誰もがよく知るExcelでできることを伝える意味で、Excelで書いた。 \(r\) を(画像では \(0.0001\) 刻みで)細かく刻んで、それぞれの \(r\) ごとの \(x\) を求めただけだ。
Figure 1: 使用したExcelファイルの冒頭
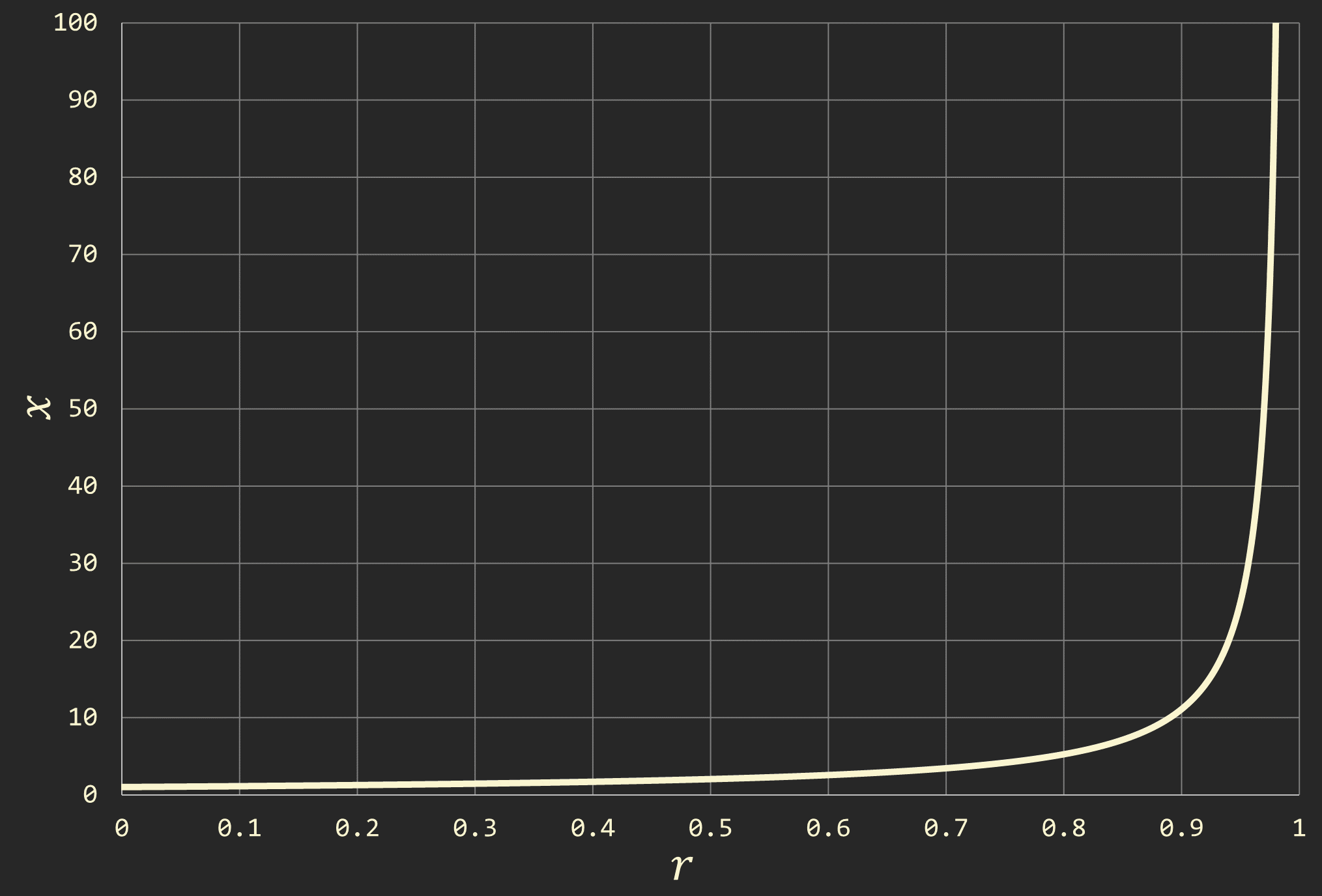
Figure 2: (d=0.01) のときの (r) - (x) グラフ
このグラフを見て分かるのは、「割合 \(r\) が 100 %に近づくにつれ、急速に \(x\) が増加する」ということである。 つまり、同じ1 %の上昇でも、1 %から2 %に上げるのと、98 %から99 %に上げるのとでは、必要なリンゴの数が桁違い であるということだ。
もしざっくり何倍になっているかが知りたければグラフから値を読み取ればいいし、正確な値が知りたければ、 先程求めた \(x\) の式に代入すればよい。このあたりは適材適所で、概観を見たい場合はグラフが役に立つし、 ある値における正確な数値が知りたければ式を使えばよいのだ。
最後に
ここまで、式変形はほぼ中学数学(文字を含む割り算はおそらく高校数学から)、 グラフを自分で考えるなら高校数学で、というくらいの難易度だった。 扱うのがこのくらいの数学でも、そこそこな議論ができる。このような、現実の問題を抽象的な概念に落とし込み、 それを解いて、再び現実の問題へと還元する、という手法は、数字の表れる様々な場面で役に立つ。 このような考え方を、頭の片隅に置いておいてほしい。